Читать книгу 📗 "Рассказы о математике с примерами на языках Python и C (СИ) - Елисеев Дмитрий Сергеевич"
Попробуем воспроизвести ее в виде программы, чтобы примерно оценить объем вычислений.
Первым шагом необходимо вычислить √12. Возникает резонный вопрос — как это сделать? Оказывается, уже в Вавилоне был известен метод вычисления квадратного корня, который сейчас так и называется «вавилонским». Суть его в вычислении √S по простой формуле:
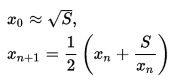
Здесь x0 — любое приближенное значение, например для √12 можно взять 3.
Запишем формулу в виде программы:
from decimal import Decimalprint ("Квадратный корень:")number = Decimal(12)result = Decimal(3)for p in range(1, 9): result = (result + number / result)/Decimal(2) difference = result**2 - number print (p, result, difference)sqrt12 = resultРезультаты весьма интересны:
Шаг | Значение | Погрешность |
1 | 3.5 | 0.25 |
2 | 3.464285714285714 | 0.00127 |
3 | 3.464101620029455 | 3.3890E-8 |
4 | 3.464101615137754 | 2.392873369E-17 |
Результат: √12 = 3,464101615137754
Как можно видеть, сделав всего 4 шага, можно получить √12 с достаточной точностью, задача вполне посильная даже для ручных расчетов 15 века.
Наконец, запрограммируем вторую часть алгоритма — собственно вычисление Пи.
sum = Decimal(1)sign = -1for p in range(1,32): sum += Decimal(sign) / Decimal((2 * p + 1)*(3**p)) sign = -sign print(p, sqrt12 * sum)print("Result:", sqrt12 * sum)Результаты работы программы:
Шаг Значение1 3.0792014356780040773821268292 3.1561814715699541793166800003 3.1378528915956803455227387694 3.1426047456630846728026494585 3.1413087854628834926354010886 3.1416743126988376716569326807 3.1415687159417842421618235548 3.1415997738115058390721497679 3.14159051093808009964275423010 3.14159330450308151312146082011 3.14159245428764630032359359712 3.14159271502037976558160621213 3.14159263454731388124271343014 3.14159265952171363845133532815 3.14159265173399758512821667116 3.14159265417257533919909221017 3.14159265340616518791967418418 3.14159265364782604643120239119 3.14159265357140338177371056520 3.14159265359563495837242748521 3.14159265358793344953097482022 3.14159265359038652271751159523 3.14159265358960362701968071024 3.141592653589853940610143646Уже на 24-м шаге мы получаем искомые 11 знаков числа Пи. Задача явно требовала больше времени чем сейчас, но вполне могла быть решена в средние века.
Современные формулы не столь просты внешне, зато работают еще быстрее. Для примера можно привести формулу Чудновского:
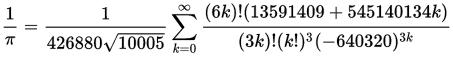
Для сравнения, те же 24 итерации по этой формуле дают число Пи со следующей точностью:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249.
Если сделать 100 итераций и вычислить 1000 знаков Пи, то можно увидеть так называемую «точку Фейнмана»:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420207
Это последовательность «999999», находящаяся на 762-м знаке от начала. Желающие могут поэкспериментировать дальше самостоятельно с помощью программы на языке Python:
from math import factorialfrom decimal import *

