Читать книгу 📗 "Курс теоретической астрофизики - Соболев Виктор Викторович"
𝑛
𝑒
𝑛⁺𝐶₁
=
4π
ε₁ν₁
ℎ
𝐸₁
⎛
⎜
⎝
χ₁
𝑘𝑇𝑒
⎞
⎟
⎠
exp
⎛
⎜
⎝
χ₁
𝑘𝑇𝑒
⎞
⎟
⎠
.
(27.8)
Введём обозначение
𝑆
𝑐
(τ)
=
𝑛𝑒𝑛⁺𝐶₁
4π𝑛₁𝑘₁ν₁
.
(27.9)
Тогда уравнения (27.7) и (27.3) принимают вид
cos θ
𝑑𝐼
ν
=-
⎛
⎜
⎝
ν₁
⎞
⎟
⎠
𝐼
ν
+
ℎ
exp
⎛
⎜
⎝
-
ℎν
⎞
⎟
⎠
𝑆
𝑐
(τ)
𝑑τ
ν
𝐸₁
⎛
⎜
⎝
χ₁
⎞
⎟
⎠
𝑘𝑇
𝑒
𝑘𝑇
𝑒
(27.10)
и
𝑆
𝑐
(τ)
=
𝑝
∞
∫
ν₁
⎛
⎜
⎝
ν₁
ν
⎞³
⎟
⎠
𝑑ν
ℎν
∫
𝐼
ν
𝑑ω
4π
+
𝑆
𝑐
⁰(τ)
,
(27.11)
где
𝑆
𝑐
⁰(τ)
=
𝑝
∞
∫
ν₁
⎛
⎜
⎝
ν₁
ν
⎞³
⎟
⎠
𝑑ν
ℎν
∫
𝐼
ν
⁰
𝑑ω
4π
(27.12)
Интенсивность излучения, приходящего от звезды в данное место туманности, очевидно, равна
𝐼
ν
⁰
=
𝐼
ν
⃰
exp
⎡
⎢
⎣
-τ
⎛
⎜
⎝
ν₁
ν
⎞³
⎟
⎠
⎤
⎥
⎦
,
(27.13)
где 𝐼ν⃰ — интенсивность излучения, выходящего из атмосферы звезды. Поэтому находим
𝑆
𝑐
⁰(τ)
=
𝑝𝑊
∞
∫
ν₁
⎛
⎜
⎝
ν₁
ν
⎞³
⎟
⎠
𝐼
ν
⃰
exp
⎡
⎢
⎣
-τ
⎛
⎜
⎝
ν₁
ν
⎞³
⎟
⎠
⎤
⎥
⎦
𝑑ν
ℎν
,
(27.14)
где 𝑊 — коэффициент дилюции излучения.
Таким образом, для определения двух искомых величин 𝐼ν(τ,θ) и 𝑆𝑐(τ) мы получили два уравнения, (27.10) и (27.11). К этим уравнениям надо добавить ещё граничные условия, которые в данном случае имеют вид
𝐼
ν
(0,θ)
=
𝐼
ν
(0,π-θ)
,
𝐼
ν
(τ₀,θ)
при
θ
>
π
2
.
(27.15)
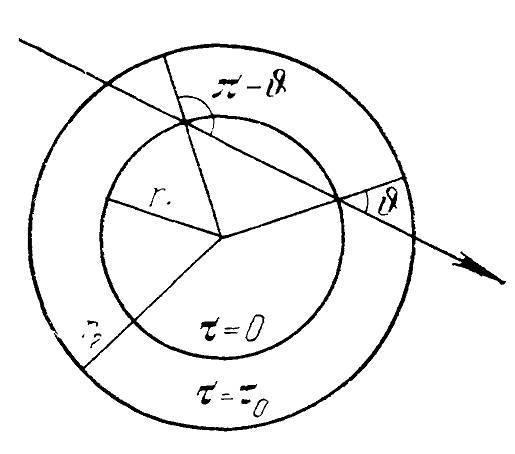
Рис. 34
Первое из этих условий, имеющее место на внутренней границе туманности (при τ=0), означает, что интенсивность излучения, выходящего из туманности, равна интенсивности излучения, входящего в туманность. Это происходит потому, что излучение, входящее в туманность в каком-либо месте на внутренней границе под углом θ к нормали, есть не что иное, как излучение, выходящее из туманности под углом π-θ на противоположной стороне (рис. 34). Второе же условие показывает, что на внешней границе туманности (при τ=τ₀) нет излучения, идущего внутрь. Из уравнения (27.10) при граничных условиях (27.15) можно найти выражение для интенсивности излучения 𝐼ν(τ,θ) через функцию 𝑆𝑐(τ). Подставляя это выражение в уравнение (27.11), получаем следующее интегральное уравнение для определения функции 𝑆𝑐(τ):
𝑆
𝑐
(τ)
=
𝑝
2
τ₀
∫
0
⎡
⎣
𝐾(|τ-τ'|)
+
𝐾(τ-τ')
⎤
⎦
×
×
𝑆
𝑐
(τ')
𝑑τ'
+
𝑆
𝑐
⁰(τ)
,
(27.16)
где
𝐾(τ)
=
∞
∫
ν₁
⎛
⎜
⎝
ν₁
ν₁
⎞
⎟
⎠
³
𝐸₁
⎡
⎢
⎣ τ
⎛
⎜
⎝
ν₁
ν₁
⎞
⎟
⎠
³
⎤
⎥
⎦ exp
⎛
⎜
⎝ -
ℎν
𝑘𝑇𝑒
⎞
⎟
⎠
𝑑ν
ν
𝐸₁
⎛
⎜
⎝
χ₁
𝑘𝑇𝑒
⎞
⎟
⎠
.
(27.17)
Уравнение (27.16) может быть изучено методами, изложенными в § 3. В частности, при τ₀ можно получить точное решение этого уравнения в явном виде.
Для упрощения рассматриваемой задачи иногда вводят средний коэффициент поглощения для всего лаймановского континуума и под τ понимают соответствующее ему оптическое расстояние. Как легко видеть, тогда вместо уравнения (27.16) имеем
𝑆
𝑐
(τ)
=
𝑝
2
τ₀
∫
0
⎡
⎣
𝐸₁|τ-τ'|
+
𝐸₁(τ-τ')
⎤
⎦
×
×
𝑆
𝑐
(τ')
𝑑τ'
+
𝑆
𝑐
⁰(τ)
.
(27.18)
Что же касается величины 𝑆𝑐⁰(τ), то её можно представить в виде
𝑆
𝑐
⁰(τ)
=
𝑝
𝑁𝑐
4π
𝑒
-τ
,
(27.19)
где 𝑁𝑐 — число квантов лаймановского континуума, падающих от звезды на 1 см² внутренней границы туманности за 1 с.
При τ₀=∞ точное решение уравнения (27.18), полученное указанным выше методом, имеет вид
𝑆
𝑐
(τ)
=
𝑝
𝑁𝑐

