Читать книгу 📗 "Курс теоретической астрофизики - Соболев Виктор Викторович"
=
1-
(1-𝐴)(1-𝐶)
1-𝐴𝐶
.
(19.79)
Для вычисления величин 𝐴₁(μ₀) и 𝐴∗ надо иметь таблицы функций φ(μ) и ψ(μ) и их нулевых и первых моментов. Такие таблицы содержатся в ряде работ (см. [3]).
Таблица 24
Сферическое альбедо 𝐴∗
𝐴
τ₀
0
0,1
0,2
0,3
0,5
1,0
2,0
3,0
∞
0
0,00
0,08
0,15
0,21
0,30
0,45
0,61
0,70
1,00
0,1
0,10
0,17
0,22
0,27
0,35
0,48
0,63
0,71
1,00
0,2
0,20
0,26
0,30
0,34
0,40
0,51
0,65
0,72
1,00
0,3
0,30
0,34
0,38
0,41
0,46
0,55
0,67
0,73
1,00
0,4
0,40
0,43
0,46
0,48
0,52
0,60
0,69
0,75
1,00
0,5
0,50
0,52
0,54
0,56
0,59
0,64
0,72
0,77
1,00
0,6
0,60
0,61
0,63
0,64
0,66
0,70
0,75
0,79
1,00
0,7
0,70
0,71
0,72
0,72
0,73
0,76
0,80
0,82
1,00
0,8
0,80
0,80
0,81
0,81
0,82
0,83
0,85
0,86
1,00
0,9
0,90
0,90
0,90
0,90
0,90
0,91
0,92
0,92
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
В таблице 24 приведены значения сферического альбедо, найденные по формуле (19.79), т.е. для того случая, когда в атмосфере оптической толщины τ₀ происходит чистое рассеяние света и атмосфера ограничена поверхностью с альбедо 𝐴.
§ 20. Оптические свойства планетных атмосфер
1. Атмосфера Венеры.
С помощью теории рассеяния света можно истолковать результаты фотометрических наблюдений планет. При этом путём сравнения теории с наблюдениями могут быть определены оптические свойства планетных атмосфер. Сначала мы сделаем это для случая атмосферы Венеры [3].
Так как через атмосферу Венеры не видна поверхность планеты, то приближённо считается, что оптическая толщина атмосферы бесконечно велика (τ₀). Для определения других величин, характеризующих оптические свойства атмосферы (в частности, индикатрисы рассеяния 𝑥(γ) и параметра λ), следует использовать наблюдаемое распределение яркости по диску планеты при разных углах фазы. Для Венеры могут быть получены особенно обширные наблюдательные данные, так как в этом случае угол фазы (т.е. угол при планете между направлениями на Солнце и Землю) принимает все возможные значения — от 0° до 180° Заключения об оптических свойствах атмосферы Венеры можно сделать и на основании кривой изменения блеска планеты с углом фазы, чем мы сейчас и займёмся.
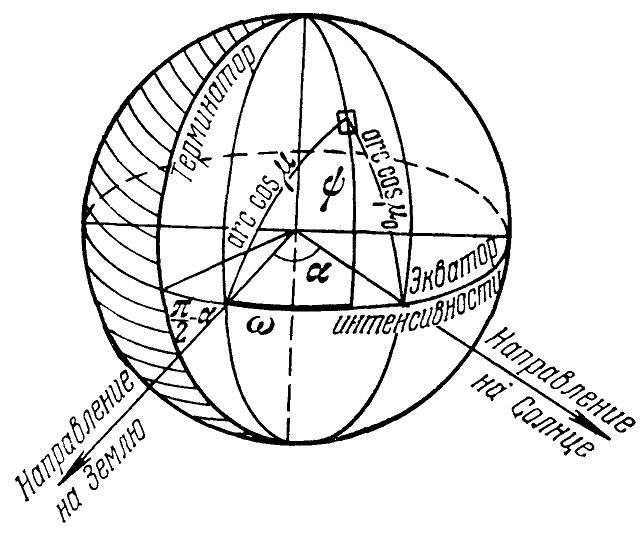
Рис. 26
Найдём теоретическую зависимость между звёздной величиной планеты 𝑚 и углом фазы α. Обозначим через μ₀ косинус угла падения солнечных лучей в данном месте планеты, через μ — косинус угла отражения и через φ — разность азимутов падающего и отражённого лучей. Введём планетоцентрические координаты ω и ψ (рис. 26). Очевидно, величины μ₀, μ, φ связаны с ω, ψ и α формулами
μ₀
=
cos
ψ
cos
(α-ω)
,
⎫
⎪
⎬
⎪
⎭
μ
=
cos
ψ
cos
ω
,
cos
α
=
μ₀
μ
-
√
(1-μ²)(1-μ₀²)
cos
φ
.
(20.1)
Пусть 𝑛𝐹 — освещённость площадки, перпендикулярной к лучам Солнца на верхней границе атмосферы планеты и ρ(μ,μ₀,φ) — коэффициент яркости атмосферы. Тогда интенсивность излучения, диффузно отражённого атмосферой, будет равна 𝐹ρ(μ,μ₀,φ)μ₀, а количество энергии, идущее от элемента площади 𝑑σ в единице телесного угла будет 𝐹ρ(μ,μ₀,φ)μμ₀ 𝑑σ. Так как 𝑑σ=𝑅²cos ψ 𝑑ψ 𝑑ω где 𝑅 — радиус планеты, то это количество энергии может быть записано в виде
𝐹𝑅²
ρ(μ,μ₀,φ)
cos(α-ω)
cos
ω
cos³ψ
𝑑ψ
𝑑ω
.
Чтобы получить полное количество энергии, идущее от Венеры в направлении Земли в единице телесного угла, надо проинтегрировать последнее выражение по ψ в пределах от -π/2 до +π/2 и по ω в пределах от α -π/2 до +π/2, т.е. от терминатора до края диска. Обозначая через Δ расстояние от Венеры до Земли, для освещённости Земли от Венеры находим
𝐸
𝑉
=
2𝐹
𝑅²
Δ²
π/2
∫
α-π/2
cos(α-ω)
cos
ω
𝑑ω
×
×
π/2
∫
0
ρ(μ,μ₀,φ)
cos³ψ
𝑑ψ
.
(20.2)
Очевидно, что освещённость Земли от Солнца равна 𝐸𝑇=π𝐹(𝑟₁/𝑟₂)², где 𝑟₁ — расстояние от Солнца до Венеры и 𝑟₁ — расстояние от Солнца до Земли, а 𝐸𝑉/𝐸𝑇=2,512𝑚☉-𝑚, где 𝑚☉ — звёздная величина Солнца. Поэтому получаем
2,512
𝑚☉-𝑚
=
2
π
⎛
⎜
⎝
𝑟₁𝑅
𝑟₁Δ
⎞²
⎟
⎠
π/2
∫
α-π/2
cos(α-ω)
cos
ω
𝑑ω
=
=
π/2
∫
0
ρ(μ,μ₀,φ)
cos³ψ
𝑑ψ
.
(20.3)
Соотношение (20.3) даёт искомую теоретическую зависимость 𝑚 от α, т.е. позволяет построить теоретическую кривую блеска планеты. В соотношение (20.3) надо подставить выражение для ρ(μ,μ₀,φ) и воспользоваться формулами (20.1). Так как коэффициент яркости ρ(μ,μ₀,φ) зависит от величин 𝑥(γ) и λ, то, сравнивая между собой теоретическую и наблюдённую кривые блеска, можно определить указанные величины. При этом следует также принять во внимание соотношение
1
2
π
∫
0
𝑥(γ)
sin
γ
𝑑γ
=
1,
(20.4)
выражающее собой условие нормировки индикатрисы рассеяния.
При определении теоретической кривой блеска удобно в выражении для ρ(μ,μ₀,φ) выделить член, учитывающий рассеяние первого порядка. В таком случае имеем
ρ(μ,μ₀,φ)
=
λ
4
𝑥(γ)
μ+μ₀
+
Δ
ρ(μ,μ₀,φ)
,
(20.5)
где γ=π-α и Δρ — член, учитывающий рассеяния высших порядков. Так как точное выражение для величины Δρ при произвольной индикатрисе рассеяния очень сложное, то мы определим эту величину приближённо, сохраняя в разложении индикатрисы рассеяния по полиномам Лежандра только два первых члена. Иными словами, величину Δρ найдём не для действительной индикатрисы рассеяния 𝑥(γ), а для индикатрисы рассеяния


